–––Creative Coding
Creative Coding
Processing ist eine grafisch orientierte Codingumgebung auf Opensource-Basis, die von Gestalter:innen und Künstler:innen gerne verwendet wird. Sie gilt als leichter Einstieg in die Welt des Codings, weil sie auf kreative Anwendungen hin konzipiert ist. Die Prinzipien aller Codingsprachen sind ähnlich und lassen sich übertragen. Processing wird als digitales Skizzenbuch verwendet, um schnell mal generative und interaktive Ideen zu testen und zu verändern. Diese Webseite begleitet den Vertiefer Creative Coding mit einer Aufgabensammlung und der Zusammenfassung von Codinganweisungen.
Struktur des Kurses
Erster Teil – Module 20.03 Processingmonster 27.03 Variable 03.04 Rechnen 17.04 Einfachschleife 08.05 Doppelschleife 15.05 Rauschen 22.05 Buchstabe und Projekt Erster Teil – Fortgeschrittene HSB-Farbraum Verzweigung Drehung Dreidimensionalität Vertexformen Zweiter Teil – Projektphase Wöchentliche individuelle Beratung
Processingmonster












Processingmonster Beispielcode
size(800, 800); background(255); // Zuerst Attribute, dann Zeichenform fill(0, 255, 0); // Attribut noStroke(); // Attribut rect(300, 250, 200, 200); // Zeichenform stroke(0, 0, 255); strokeWeight(4); line(350, 250, 300, 200); line(450, 250, 500, 200); fill(255, 255, 0); stroke(0, 0, 255); strokeWeight(10); ellipse(300, 200, 50, 50); fill(255, 0, 255); ellipse(500, 200, 50, 50); line(350, 450, 350, 500); line(400, 450, 400, 500); line(450, 450, 450, 500); fill(255, 255, 0); arc(400, 350, 100, 100, radians(0), radians(180)); fill(0, 255, 0); noStroke(); triangle(250, 350-50, 250-50, 350, 250+50, 350); triangle(550, 350-50, 550-50, 350, 550+50, 350); stroke(0, 0, 255); strokeWeight(4); noFill(); bezier(400, 250, 400, 250, 450-100, 100, 450, 100); fill(255, 0, 0); stroke(0, 255, 255); strokeWeight(10); ellipse(450, 100, 50, 50);
Zeichenformen
Zeichenfenster in Pixeln
size (800, 800);
Hintergrundfarbe als Graustufe
background (255);
Rechteck
rect (x, y, breite, hoehe);
Linie
line (ax, ay, bx, by);
Kreis
ellipse (x, y, breite, hoehe);
Kreisbogen
arc (x, y, breite, hoehe, anfangswinkel, endwinkel);
Dreieck
triangle (ax, ay, bx, by, cx, cy);
Reckteck
rect(x, y, breite, hoehe);
Bezierlinie
bezier(ax, ay, ctrl_ax, ctrl_ay, ctrl_bx, ctrl_by, bx, by);
Kreis
ellipse(x, y, breite, hoehe);
Attribute
Füllfarbe als RGB
fill (0, 255, 0);
Keine Kontur
noStroke();
Konturfarbe als RGB
stroke (0, 0, 255);
Konturstärke
strokeWeight(4);
–––
Einleitung
Video
Worum geht es im Kurs ?
Gestalten mit Processing handelt von Generativer Gestaltung und hat zum Ziel experimentelle Buchstabenbilder zu erstellen. Anhand eines Buchstaben lernen wir die Grundlagen der visuell orientierten Programmiersprache Processing kennen. Der Inhalt der ersten Semesterhälfte ist in Modulen aufbereitet und wird von Aufgaben und dieser begleitenden Webseite ergänzt. Zu jedem Modul wird es ein Video geben. In der zweiten Semesterhälfte folgt die Projektphase. Hier wenden wir das erworbene Modulwissen in einer gestalterischen Experimentierreihe auf einen Buchstaben an. Das Wahlpflichtfach ist ab dem drittem Semester wählbar und Teil des Curriculums an der Hochschule Mannheim.
zurück zur Übersicht
–––
Variable
Video
Was sind Variablen ?
Variablen sind ein Grundkonzept der Informationsverarbeitung. Wir nutzen Variablen, um Information in ihnen zu speichern. Diese ist dynamisch und verändert sich im Laufe eines Programm durch Berechnungen. Bevor wir Variablen in Processing verwenden können, stellen wir diese einem Computer mit einem virtuellen coronafreien Handshake vor.
Methoden und Parameter

size(800, 800);
println ("Hallo Welt");
ellipse (400, 400, 500, 500);
Datentypen
Ganze Zahl
int
Zahl mit Nachkommastelle
float
true oder false
boolean
Einzelner Buchstaben
char
Wort oder Satz
String
Daten in Variablen speichern
float katzen;
katzen = 12;
float hunde = 3;
float maeuse = 10;
float tiere;
tiere = katzen + hunde + maeuse;
println ("Tiere: " + tiere);
Variablen verschiedenen Datentyps
int stueckzahl = 12;
float menge = 2.1;
boolean pendel = true;
char initiale = 'T';
String wort = "Thorsten";
println("Obst: " + stueckzahl);
println("Wasser: " + menge + " Liter");
println("Wahrsager: " + pendel);
println("Anfangsbuchstabe: " + initiale);
println("Vorname: " + wort);
Aufgaben
Variable / Warmup
Kopiere die mitgelieferten Beispielcodes "Methoden und Parameter", "Daten in Variablen speichern" und "Variablen verschiedenen Datentyps". Teste jedes der drei Programme mit unterschiedlichen Variablenwerten und Variablennamen. Starte bei jeder Veränderung eines Variablenwertes und Variablennamens das Programm neu.
Variable / Aufgabe 1
Erstelle ein neues Programm mit zwei Variablen des Datentyps String – eine für den Vornamen und eine weitere für den Nachnamen. Erstelle eine dritte Variable des Datentyps String für den Gesamtnamen. Addiere den Vornamen und den Nachnamen und speichere das Ergebnis im Gesamtnamen. Lass dir den Inhalt des Gesamtnamens im Kontrollfenster anzeigen. Drücke dazu den Play-Button im Processingfenster links oben - damit startest du das Programm. Es wird Zeile für Zeile ausgeführt. Nach Ausführung der letzten Zeile stoppt das Programm automatisch.
Variable / Aufgabe 2
Definiere drei Variablen des Datentyps int mit den Variablennamen a, b und division. Weise der Variable a den Wert 11 und der Variable b den Wert 2 zu. Dividiere a durch b und speichere das Ergebnis in division. Lass dir den Inhalt der Variable division im Kontrollfenster anzeigen. Warum produziert dieses Programm ein falsches Ergebnis ? // Schreibe deine Begründung als Kommentar ins Programm – einen Kommentar markierst du in Processing mit einem vorangestellten doppelten Schrägstrich.
Variable / Aufgabe 3
Definiere mehrere Variablen des Datentyps float mit den Variablennamen a, b, summe, differenz, multiplikation und division. Weise a und b jeweils einen Variablenwert zu. Addiere a mit b und speichere das Ergebnis in der Variable summe. Subtrahiere b von a und speichere das Ergebnis in der Variable differenz. Multipliziere a mit b und speichere das Ergebnis in der Variable multiplikation. Das Zeichen fürs Multiplizieren ist ein Stern. Teile a durch b und speichere das Ergebnis in der Variable division. Das Zeichen fürs Teilen ist ein Schrägstrich den du am Mac mit SHIFT + 7 erzeugst. Lass dir nach den Berechnungen alle Variablenwerte inklusive a und b im Kontrollfenster anzeigen. Beschrifte hierzu mit der Methode println jeden Variablenwert mit vorangestelltem Text.
Variable / Aufgabe 4
Du hast in Aufgabe 4 die Minimalversion eines Taschenrechners erstellt. Verändere die Werte von a und b und starte das Programm jeweils neu.
Variable / Aufgabe 5
Erstelle ein neues Programm mit einer Variable des Datentyps boolean – die Variable soll den Namen kristallkugel tragen. Weise der Variable kristallkugel den Wert true zu. Lass dir den Inhalt von kristallkugel im Kontrollfenster anzeigen. Weise danach der Variable kristallkugel den Wert false zu. Lass dir den Inhalt der Variable erneut im Kontrollfenster anzeigen. Die Lösung der Aufgabe soll vier Zeilen umfassen. Du darfst nur eine Kristallkugel verwenden.
Variable / Aufgabe 6
Entwerfe auf Grundlage des bisherigen Inputs eine eigene Idee und formuliere diese als Programm.
Handshake
Daten speichern wir in Variablen. Um unterschiedliche Daten zu erfassen, stehen uns in Processing verschiedene Datentypen zur Verfügung: int für ganze Zahlen, float für Nachkommazahlen, String für Wörter, char für Buchstaben, boolean für einen Zustand der wahr oder falsch sein kann. Um eine Variable in Processing zu verwenden, müssen wir diese zuerst dem Computer mit einem Handshake vorstellen. Dazu nennen wir zuerst den Datentyp, den die Variable haben soll und fügen durch ein Leerzeichen getrennt einen frei wählbaren Variablennamen hinzu. Jede Zeile in Processing schließen wir mit einem Semikolon ab, was einem Punkt in der geschriebenen klassischen Sprache entspricht.
Zuweisen
Daten bestehen aus Werten. Um einen Wert in einer Variable zu speichern brauchen wir ein Gleichheitszeichen: Links des Gleichheitszeichens schreiben wir den Variablennamen und rechts davon einen Wert. Dies bezeichnet man als Zuweisen. Der Wert kann eine Zahl, ein Wort, ein Buchstabe oder ein Zustand sein. Es hängt davon ab, welchen Datentyp wir für unseren Variablennamen zuvor gewählt haben.
Rechnen
Wir können rechts des Gleichheitszeichens statt eines Wertes ebenfalls Variablen hinschreiben und diese durch Grundrechenarten zu einem mathematischen Ausdruck verbinden. In einem laufenden Program werden die Variablen auf der rechten Seite durch den Wert der ihnen zuvor zugewiesen wurde ersetzt. Das passiert unsichtbar im Hintergrund. Stehen bleibt ein mathematischer Ausdruck der berechnet wird und als neuer Wert der Variable auf der linken Seite zugewiesen wird. Im Beispiel wird die Anzahl von Katzen, Hunden und Mäusen in der Variable Tiere gespeichert.
Methoden und Parameter
Mit der Methode ellipse zeichnen wir einen Kreis auf eine Zeichenfläche. Mit der Methode println lässt sich der Wert einer Variable im schwarzen Kontrollfenster von Processing anzeigen. Wir übergeben an eine Methode Parameter durch ein Komma getrennt und durch runde Klammern zusammengefasst. Die Methode ellipse braucht vier Parameter. Die Reihenfolge gibt deren Deutung vor. Der erste Parameter ist der x-Wert der Ellipse, der zweite der y-Wert, der dritte die Ellipsenbreite und der vierte die Ellipsenhöhe. Bei der Methode println übergeben wir Text oder Variablen als Parameter, Text in Anführungszeichen, Variablen ohne. Variablen und Text kombinieren wir durch ein Pluszeichen. Das Pluszeichen klebt – ohne Leerzeichen - den Wert der Variable unmittelbar an den Text im Kontrollfenster.
Weiterführende Themen
Ein Array ist die nächsthöhere Organisationseinheit für Variablen. Mehrere Variablen können in einem sogenanntem Feld gespeichert werden. In Verbindung mit Schleifen, die du bald kennenlernen wirst, kannst du Daten in einem Array auf eine effiziente Art speichern und wieder abrufen.
–––
Rechnen
Video
Wie rechnen wir in Processing ?
Um Bilder in Processing zu zeichnen, beschreiben wir sie mit einer formalen Abfolge logischer Verknüpfungen und relativer Bezüge ihrer gestalterischen Elemente untereinander. Das macht sie erst dynamisch und skalierbar. Dafür brauchen wir Variablen – darin speichern wir Werte. In Variablen und in Parametern von Methoden rechnen wir anschließend und erzeugen eben jede Verknüpfungen und Bezüge.
Parameteraddition

size(800, 800);
int radius = 250;
int mitteX = 400;
int mitteY = 400;
noFill();
ellipse (mitteX, mitteY, radius, radius);
ellipse (mitteX, mitteY, radius + 250, radius + 250);
Variablenaddition

size(800, 800);
int radius = 250;
int mitteX = 400;
int mitteY = 400;
noFill();
ellipse (mitteX, mitteY, radius, radius);
radius = radius + 250;
ellipse (mitteX, mitteY, radius, radius);
Relativ statt Absolut
int x = 50;
int y = 50;
line (x, y, x + 20, y - 20);
Grundrechenarten
Variablenaddition
radius = radius + 1;
Variablensubtraktion
radius = radius - 1;
Variablendivision
radius = radius / 4;
Variabelenmultiplikation
radius = radius * 4;
Parameteraddition
ellipse(400, 400, radius + 1, radius + 1);
Parametersubtraktion
ellipse(400, 400, radius - 1, radius - 1);
Parameterdivision
ellipse(400, 400, radius / 4, radius / 4);
Parametermultiplikation
ellipse(400, 400, radius * 4, radius * 4);
Codebeispiel
int radius = 7;
radius = radius + 1;
radius = radius * 4;
println("radius " + radius);
Aufgaben
Rechnen / Warmup
Kopiere die mitgelieferten Beispielcodes "Parameteraddition", Variablenaddition" und "Variablenaddition und Division". Teste jedes der drei Programme mit unterschiedlichen Variablenwerten. Starte bei jeder Veränderung eines Variablenwertes das Programm neu.



Rechnen / Aufgabe 1
+
-
Verwende drei Variablen, um einen Kreis zu zeichnen: eine für den Kreisradius radius, eine für x-Position mitteX und eine für die y-Position der Kreismitte mitteY.
Erstelle mit der Methode size eine 800 mal 800 Pixel große Zeichenfläche. Definiere drei Variablen des Datentyp float – eine für den Kreisradius mit dem Namen radius, eine für die x-Position der Kreismitte mit dem Namen mitteX und eine für die y-Position des Kreismitte mit dem Namen mitteY. Weise mitteX, mitteY und radius jeweils den Variablenwert 400 zu. Verwende die Methode noFill um vom folgenden Kreis nur die Outline zu zeichnen. Verwende die Methode ellipse mit den erstellten Variablen als Parameter, um einen Kreis auf der Zeichenfläche zu zeichnen.
Rechnen Aufgabe 2
+
-
Erweitere Aufgabe 1. Zeichne einen weiteren Kreis links und einen weiteren rechts vom ersten. Verwende dazu eine weitere Variable für den Abstand zwischen zwei Kreisen mit dem Namen abstand und eine Parameteraddition sowie eine Parametersubtraktion.
Erweitere Aufgabe 1. Zeichne einen zweiten Kreis rechts vom ersten Kreis mit der Methode ellipse und einer Parameteraddition – verändere die Kreisposition um 150 Pixel. Zeichne einen dritten Kreis links vom ersten Kreis mit der Methode ellipse und einer Parametersubtraktion – verändere die Kreisposition ebenfalls um 150 Pixel.
Rechnen / Aufgabe 3
+
-
Erweitere Aufgabe 2. Zeichne einen weiteren Kreis oben und einen weiteren unten. Verwende dazu die Variable abstand und erneut eine Parameteraddition sowie eine Parametersubtraktion.
Erweitere Aufgabe 1. Erstelle eine neue Variable des Datentyps float für den Abstand zwischen zwei Kreisen mit dem Variablennamen abstand. Weise der Variable abstand den Variablenwert 150 zu. Ersetze in der Parameteraddition den konstanten Wert – um den du den zweiten Kreis nach links verschoben hast – durch die Variable abstand. Ersetze bei deinem dritten Kreis in der Parametersubtraktion den konstanten Wert ebenfalls durch die Variable abstand. Zeichne einen vierten Kreis oberhalb des mittleren Kreises – verwende dazu die Methode ellipse, eine Parametersubtraktion und die Variable abstand. Zeichne einen fünften Kreis unterhalb des mittleren Kreises – verwende dazu die Methode ellipse, eine Parameteraddition und ebenfalls die Variable abstand.
Rechnen / Aufgabe 4
Du hast in Aufgabe 3 deine erste minimalistische generative Grafik erstellt. Die Regel ordnet die fünf Kreise in einem Kreuzmuster gleichabständig an. Der Abstand zwischen zwei Kreisen ist der Parameter, der deiner Grafik eine Varianz verleiht. Teste den Abstand zwischen zwei Kreisen mit verschiedenen Werten für die Variable abstand und starte das Programm jeweils neu.
Rechnen / Aufgabe 5
Erstelle ein neues generatives Muster nach dem gleichen Prinzip. Verwende einen Kreis als Ursprungselement und bestimmte die Position der nachfolgenden Kreise mit Parameterveränderungen.
Variable mit Selbstbezug
Bisher haben wir so gerechnet, dass wir auf der rechten Seite des Gleichheitszeichens andere Variablen hatten als auf der linken Seite. Wir können den Wert einer Variable auch in der Art verändern, dass wir die Variable von der linken Seite des Gleichheitszeichen auf der rechten Seite wiederholen und dieser beispielsweise einen Wert hinzu addieren, subtrahieren, durch einen Wert teilen oder mit einem Wert multiplizieren. In diesem Fall wird die Variable in einem laufenden Programm auf der rechten Seite durch einen Wert ersetzt, den wir ihr zuvor zugewiesen haben. Auf der rechten Seite bleibt danach ein mathematischer Ausdruck stehen, der berechnet wird und der Variable auf der linken Seite zugewiesen wird. Der neue Wert überschreibt den alten Wert.
Parameteraddition und Variablenaddition
Verändern wir den Wert einer Variable durch ein Gleichheitszeichen mit einer der vier Grundrechenarten, so sprechen wir von Variablenaddition, Variablensubtraktion, Variablendivision oder Variablenmultiplikation. Verändern wir einen Parameter in einer Methode mit einer der Grundrechenarten, so sprechen wir von Parameteraddition, Parametersubtraktion, Parameterdivision oder Parametermultiplikation. Wenn wir also als Parameter einer Methode eine Variable einsetzen und diese durch eine Grundrechenart verändern, so bleibt der Wert der Variable unverändert. Im laufenden Programm wird die Variable durch einen Wert ersetzt, der ihr zuvor zugewiesen wurde. Es bleibt ein mathematischer Ausdruck stehen der zusammengerechnet wird, jedoch wird das Ergebnis nicht in einer Variable gespeichert, da hier das Gleichheitszeichen fehlt. Eine Parameterrechnung wirkt demnach punktuell in einer Methode wie beispielsweise ellipse, eine Variablenrechnung wirkt dagegen nachhaltig, indem sich der Wert der Variable ändert.
zurück zur Übersicht–––
Aufbau
Video
Wie ist ein Programm in Processing aufgebaut ?
Ein Koordinatensystem der Informatik unterscheidet sich vom Koordinatensystem der Mathematik. Wir beschreiben Punkte absolut und relativ zueinander, um uns in einem Koordinatensystem zu bewegen. Außerdem schauen wir uns den Aufbau eines Programms in Processing an. Er kann linear oder strukturiert sein. Ein strukturierter Aufbau teilt das Programm in einen Setup- und einen Draw-Bereich. Während wir im Setup-Bereich allgemeine einmalige Einstellungen eintragen, schreiben wir im Draw-Bereich unser eigentliches Programm. Oberhalb von Setup stellen wir globale Variablen vor, die wir im Programm verwenden wollen.

Linear
int x = 50;
size(100, 100);
background(255);
noFill();
ellipse (x, 50, 75, 75);
noLoop
int x = 50;
void setup() {
size(100, 100);
background(255);
noLoop();
}
void draw() {
noFill();
ellipse (x, 50, 75, 75);
}
Loop
int x = 50;
void setup() {
size(100, 100);
background(255);
}
void draw() {
noFill();
ellipse (x, 50, 75, 75);
}
Übung Master und Servant


Master and Servant spielt ihr zu zweit – es geht auch zu dritt. Wichtig ist, dass jeder einmal Master und einmal Servant spielt. Jeder downloadet zunächst ein Master-Blatt und ein Servant-Blatt. Auf beiden Blättern ist jeweils ein Koordinatensystem abgebildet. Jeder erstellt für sich auf seinem Masterblatt eine Ein-Linien-Zeichnung, die ein Bild oder ein Symbol darstellt – das Servantblatt bleibt dagegen frei. Das Symbol kannst du auch in mehrere Ein-Linien-Zeichnungen zerlegen, wie in der Beispielzeichnung der Klopapierrolle. Nun teilt ihr euch in Zweier-Gruppen auf und spielt eine Master-Servant-Kommunikation jeweils zweimal mit vertauschten Rollen – jeder ist einmal Master und einmal Servant. Der Master gibt dem Servant Befehl für Befehl die Zeichnung durch. Der Servant versucht zu erraten, um was für ein Bild oder Symbol es sich handelt, bevor der Master seine Anweisungen ganz durchgefunkt hat. Die erste Koordinatenangabe einer Ein-Linienzeichnung ist dabei absolut zum Beispiel 20, 30. Alle nachfolgenden Anweisungen relativ zum vorhergehenden Punkt zum Beispiel +50, -20. Der Servant verbindet nach jedem durchgegebenen Befehl den neuen Punkt mit dem vorhergehendem Punkt mit einer Linie. Verwende zum Übertragen der Befehle Textmessages per WhatsApps – der Servant darf seine Zeichnung seinem Master zwischendurch als Bild per WhatsApp schicken und den Master um Rat und Richtigkeit des Befehls und der Zeichnung fragen. Die beiden Übungsblätter druckst du entweder aus oder öffnest sie in Illustrator, um in einer neuen Ebene mit dem Bezierwerkzeug Linien zu zeichnen. Der Soundtrack als Video zur Übung Download Master-Blatt PDF Download Servant-Blatt PDF
Übung Drag-and-Drop Codezeilen
Bringe die Codezeilen per Drag and Drop in die richtige Reihenfolge. Zur interaktiven Übung
Aufgaben
Aufbau / Warmup
Kopiere den Code von "Linear" und starte das Programm. Kopiere den Code von "noLoop". Verwende die Tastenkombination APFEL + T, um den Code automatisch mit Tabulatoren einzurücken und aufzuräumen. Starte das Programm. Kopiere den Code von "Loop", verwende APFEL + T und starte das Programm. Siehst du den Unterschied in der Darstellung des Kreises in "Loop" im Vergleich zu den anderen beiden Codes "noLoop" und "Linear" ? In "Loop" wird der Kreis unendlich oft übereinander gezeichnet – solange das Programm läuft.
Aufbau / Aufgabe 1
Kopiere den Code von "Loop". Füge nach der Methode ellipse – jedoch vor der schließenden geschweiften Klammer – eine neue Zeile ein: Wende eine Variablenaddition auf die Variable x an – erhöhe dazu den Wert der Variable x um 5. Starte das Programm.
Aufbau / Aufgabe 2
Kopiere den Code von "noLoop". Füge analog zu Aufgabe 1 eine Variablenadditon für die Variable x hinzu. Starte das Programm.
Aufbau / Aufgabe 3
Verwende den modifizierten Code aus Aufgabe 1. Lösche die Methode background aus dem setup-Bereich und füge sie als erste Zeile in den draw-Bereich ein; nach der sich öffnenden geschweiften Klammer und vor noFill . Starte das Programm – Das ist der Animations- und Interaktionsmodus.
Aufbau / Aufgabe 4
Das folgende Programm ist im linearen Modus aufgebaut. Es verwendet die Methode line, um Linien von einem zum nächsten Punkt zu zeichnen. Ausgehend von einem absoluten Punkt werden die nachfolgenden Punkte immer relativ zum absoluten Ausgangspunkt beschrieben. Schreibe das Programm in einen strukturierten Modus unter Einsatz von noLoop um. size(400, 400); float x, y; x = 100; y = 200; line(x, y, x + 100, y - 100); line(x + 100, y - 100, x + 200, y); line(x + 200, y, x + 100, y + 100); line(x + 100, y + 100, x, y);
Koordinatensystem
Unsere Zeichenfläche in Processing besteht aus einem Koordinatensystem mit einer x-Achse und einer y-Achse. Die y-Achse wird in der Informatik im Gegensatz zur Mathematik umgedreht verwendet, mit positiven Zahlen im unteren Bereich und negativen Zahlen im oberen Bereich. Mit der Methode size legen wir die Größe unserer Zeichenfläche fest, mit der Methode background die Hintergrundfarbe.
Standbild und Interaktionsmodus
Die meisten Beispiele dieser Lektionen verwenden einen vereinfachten linearen Aufbau, der für die Erzeugung von Standbildern genügt. Hierbei arbeitet sich das Programm von der obersten bis zur untersten Zeile durch und bleibt danach stehen. Bei interaktiven Projekten und beim Einsatz von externen Bibliotheken brauchen wir einen interaktiven Modus. Dieser Modus besteht aus einem setup-Bereich und einem draw-Bereich. Beide Bereiche werden mit dem Schlüsselwort void gekennzeichnet. Der setup-Bereich läuft zu Beginn einmal durch und enthält allgemeingültige Voreinstellungen. Danach folgt der draw-Bereich, dessen Inhalt dauerhaft wiederholt wird, beispielweise um die Mausposition zu ermitteln. Wir können den Loop des draw-Bereichs mit der Methode noLoop im setup-Bereich unterbinden. Der interaktive Modus verhält sich in diesem Fall wie der lineare Modus.
zurück zur Übersicht–––
Grundform
Video
Welche Grundformen gibt es in Processing ?
Punkt, Linie, Rechteck, Ellipse, Bogen und Bezierkurve sind die wichtigsten Grundformen in Processing mit denen wir unsere generativen Grafiken aufbauen – und es gibt noch mehr Zeichenformen. Zwei Grundformen lassen sich zu neuen elementaren Zeichenformen verbinden. Mit Attributen wie Füllfarbe, Konturfarbe, Strichstärke und Transparenz beeinflussen wir die optischen Eigenschaften von Grundformen. Dabei folgen wir einer einfachen Regel. Wir nennen zuerst das Attribut – erst danach zeichnen wir die Form. Farbe ist von Form unabhängig. Welche Farbe ein Element annimmt, hängt von der Position im Programmverlauf ab, an der wir ein Attribut setzen. Das gesetzte Attribut wirkt solange fort, bis wir ein neues festlegen.
Punkt

size(800, 800);
float px = 400;
float py = 400;
strokeWeight(3);
point (px, py);
Linie

size(800, 800);
float ax = 150;
float ay = 400;
float bx = 650;
float by = 400;
line (ax, ay, bx, by);
Kreis

size(800, 800);
float mitteX = 400;
float mitteY = 400;
float breite = 500;
float hoehe = 500;
ellipse (mitteX, mitteY, breite, hoehe);
Kreisbogen

size(800, 800);
float mitteX = 400;
float mitteY = 400;
float breite = 500;
float hoehe = 500;
float start = radians(0); // Startwinkel
float ende = radians(270); // Endwinkel
arc (mitteX, mitteY, breite, hoehe, start, ende);
Rechteck

size(800, 800);
float eckeX = 150;
float eckeY = 150;
float breite = 500;
float hoehe = 500;
rect (eckeX, eckeY, breite, hoehe);
Bezier

size(800, 800);
float ax = 200;
float ay = 600;
float bx = 200;
float by = 300;
float cx = 300;
float cy = 200;
float dx = 600;
float dy = 200;
bezier(ax,ay,bx,by,cx,cy,dx,dy);
Attribute

size (800, 800);
int radius = 200;
int mitteX = 400;
int mitteY = 400;
noFill();
stroke (0, 0, 255);
ellipse (mitteX, mitteY, radius*3, radius*3);
stroke (0, 255, 255);
ellipse (mitteX, mitteY, radius*2, radius*2);
stroke (255, 0, 255);
ellipse (mitteX, mitteY, radius, radius);
Attribute
Flächengraustufe 0 bis 255
fill(255);
Flächenfarbe(RGB) 0 bis 255
fill(0,0,255);
Keine Füllung
noFill();
Konturgraustufe 0 bis 255
stroke(0);
Konturfarbe(RGB) 0 bis 255
stroke(0,0,255);
Konturstärke 0.1 bis ...
strokeWeight(1);
Keine Kontur
noStroke();
Graustufentransparenz 0 bis 255
fill(255,100);
Farbtransparenz 0 bis 255
fill(0,0,255,100);
Aufgaben
Grundform / Warmup
Kopiere die mitgelieferten Beispielcodes. Teste jedes der Programme mit unterschiedlichen Variablenwerten und unterschiedlichen Attributen. Starte bei jeder Veränderung eines Variablenwertes oder Attributwertes das Programm neu.
Grundform / Aufgabe 1
Schreibe die Codebeispiele für Punkt, Linie, Kreis, Kreisbogen, Rechteck und Bezier um. Verwende ausschließlich Konstanten statt Variablen, um die verschieden Formen zu zeichnen. Lösche anschließend die verwendeten Variablen aus dem Code.
Grundform / Aufgabe 2a bis 2d
+
-

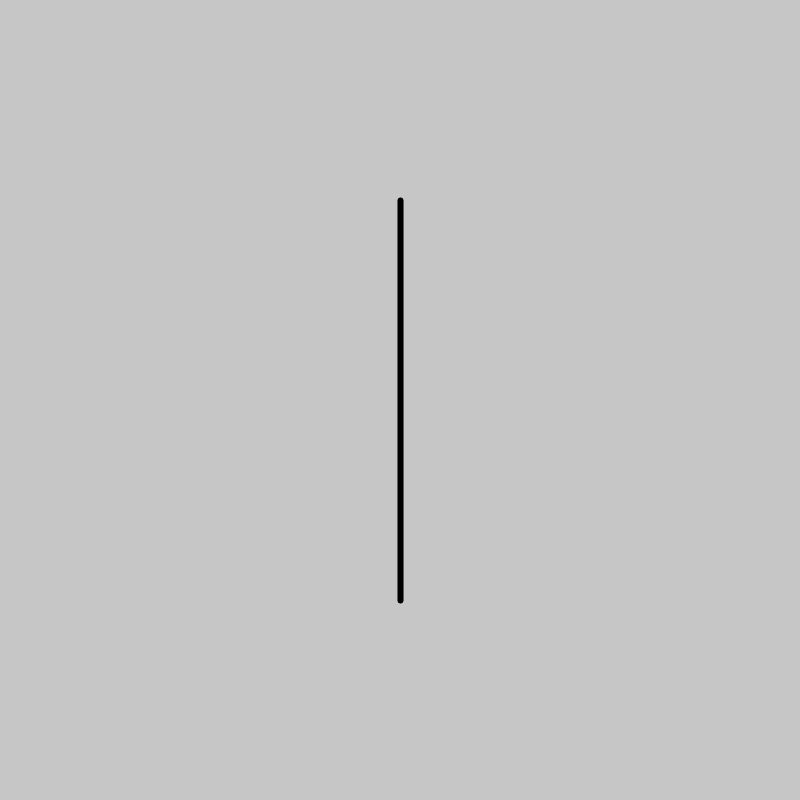


Zeichne vier verschiedene Linien von ihrem Mittelpunkt aus. Verwende für den Mittelpunkt die Variablen x und y. Bestimme die Eckpunkte der Linien relativ zum Mittelpunkt mit Parameteraddition und Parametersubtraktion.
Erstelle mit der Methode size eine 800 mal 800 Pixel große Zeichenfläche. Definiere zwei Variablen des Datentyp int mit den Variablennamen x und y. Weise der Variable x den Wert 400 zu. Weise der Variable y ebenfalls den Wert 400 zu. Verwende ausgehend von den Variablen x und y die Methode line sowie Parameteraddition beziehungsweise Parametersubtraktion, um jeweils eine Linie zu zeichnen.
Grundform / Aufgabe 3a und 3b
+
-

Erstelle einen Kreisbogen mit der Methode arc. Es gibt zwei Wege, die Winkel zu bestimmen, um die Aufgabe zu lösen.
Erstelle einen Kreisbogen mit der Methode arc. Beachte, dass 0° auf 3 Uhr liegt und Winkelangaben im Uhrzeigersinn ansteigen – dabei fällt 360° mit 0° zusammen. Es ist jedoch zum einen möglich, Winkelangaben größer als 360° anzugeben, zum anderen ist es möglich, negative Winkel anzugeben. Es gibt also zwei Wege die Aufgabe zu lösen. Führe beide Wege aus. Weiterhin ist es nicht notwendig, im Kopf zu rechnen – denn radians(360 + 90) führt zum selben Ergebnis wie radians(450).
Grundform / Aufgabe 4
+
-

Zeichne drei Kreise mit einem gemeinsamen Mittelpunkt. Verwende dazu drei Variablen radius, mitteX und mitteY. Zeichne zuerst den kleinen Kreis, dann den mittleren und zum Schluß den großen. Gib dem mittleren Kreis eine größere Strichstärke.
Erstelle eine 800 mal 800 Pixel große Zeichenfläche. Definiere drei Variablen des Datentyps float mit den Variablennamen mitteX, mitteY und radius. Weise den Variablen mitteX und mitteY jeweils den Variablenwert 400 zu. Weise der Variable radius den Wert 500 zu. Verwende die Methode noFill, um Konturen ohne Füllung zu zeichnen. Verwende die Methode ellipse mit den Variablen mitteX, mitteY und radius als Parameter, um einen Kreis zu zeichnen. Verwende eine Variablendivision für radius – teile dazu radius durch den Faktor 1.5 und weise das Ergebnis radius erneut zu. Kopiere die beiden zuletzt erstellten Anweisungen – Methode ellipse und die Variablendivision – zweimal um zwei weitere Kreise zu zeichnen. Stelle beim mittlerem Kreis eine andere Strichstärke ein.
Grundform / Aufgabe 5
Erstelle ein neues Zeichen durch Kombination aus vorhandenen Grundformen. Lege hierzu den Mittelpunkt des Zeichens als zwei Variablen mitteX und mitteY an. Lege alle weiteren Positions- und Größenangaben relativ zu diesem Mittelpunkt an. Auf diese Weise wirst du das neue Zeichen später leicht verschieben können.
Grundformen
Uns stehen verschiedene geometrische Grundformen als Methoden zur Verfügung wie Punkt, Linie, Kreis, Quadrat und andere. Jede Methode braucht eine andere Anzahl an Parametern, damit sie funktioniert. Ein Punkt braucht zwei Parameter, eine Ellipse vier. Bei manchen Methoden variiert die Anzahl. Die Methode fill färbt bei einem Parameter Objekte in Graustufen, bei drei Parametern Objekte in Farbe.
Attribute
Attribute beeinflußen Farbe, Strichstärke und Transparenz von Objekten. Mit fill färben wir die Füllung von Objekten, mit stroke die Kontur. Mit noFill entfernen wir die Füllung, mit noStroke die Kontur. Für Transparenz geben wir zusätzlich zur Farbe oder zur Graustufe einen weiteren Parameter an. Mit strokeWeight bestimmen wir die Strichstärke der Kontur. Generell sind bei Programmstart Attribute ohne unser weiteres Zutun voreingestellt. So ist der Hintergrund mittelgrau, Flächenfüllungen weiß und Konturen schwarz. Man kann sich die Attributsammlung als einen bunten Blumenstrauß vorstellen, der immer auf einmal wirkt. Ändern wir im Verlauf unseres Codes ein Attribut, verändern wir auch die Gesamtheit des Blumenstraußes: Die Wirksamkeit bleibt fortbestehen – bis zum Zeitpunkt einer erneuten Änderung. Attibutänderungen wirken sich immer nur auf nachfolgende Objekte aus, nicht auf vorhergehende. Man kann sich die Codezeilen wie Ebenen vorstellen, die aufeinander abgelegt werden. Je früher eine Zeile geschrieben wurde, desto weiter unten befindet sie sich.
Möchten wir beispielsweise drei Kreise in rot, grün und blau nebeneinander zeichnen, verwenden wir vor jeder neuen Methode ellipse jeweils einen neue Methode fill für jede neue Farbe. Zeichnen wir im Anschluss weitere Kreise ohne einen erneuten fill-Befehl, bleibt die zuletzt eingestellte Füllfarbe – bis wir diese erneut ändern.
Absolut und Relativ
Bei der Angabe von Koordinaten können wir zum einem zwischen Konstanten und Variablen unterscheiden, zum anderen zwischen absoluten Koordinaten und relativen Koordinaten. Absolute Koordinaten geben einen festen Ort an, entweder durch eine Konstante oder eine Variable. Relative Koordinaten geben einen zweiten Ort, der mit einem ersten verbunden ist. Verändern wir den ersten Ort, verändert sich der zweite automatisch mit. Ein gutes Beispiel dafür ist eine Linie die aus zwei Punkten besteht. Den ersten Punkt geben wir durch die Variablen x und y an. Den zweiten Punkt geben wir durch einen Parameterrechung an – beispielsweise eine Parameteraddition und -subtraktion. Mit x + 100 und und y - 100 zeichnen wir eine Diagonale, die in einem 45 Grad Winkel nach rechts oben verläuft. Ändern wir den ersten Punkt, indem wir die Werte von x und y verändern, wird der zweite Punkt automatisch berechnet. Relative Angaben sind effizient und ein grundlegendes Prinzip, um Zusammenhänge zwischen Objekten zu abstrahieren. Konstante Angaben entsprechen eher der händischen Arbeit, die wir aus den klassischen Grafikprogrammen kennen: Das kostet viel Zeit.
Weiterführende Themen
triangle(), curve(), vertex(), quad() sind weitere Zeichenmethoden, die du dir anschauen solltest. Insbesondere wenn du organisch wirkende und gebogene Formen erstellen möchtest, wirst du entweder die Methode curve() oder bezier() brauchen. Es lohnt sich aufwändige Zeichenformen einzusetzen, weil diese oft überraschendere Ergebnisse liefern.
–––
Export
Video
Welche Bildformate können wir mit Processing exportieren ?
In Processing erzeugte Bilddaten können wir in unterschiedlichsten Formaten exportieren. Wir beschränken uns auf den Export von Pixeldaten und Vektordaten. Während wir Pixeldaten in 72 dpi Auflösung als JPG, TIFF und PNG exportieren, steht uns für Vektordaten das PDF-Format zur Verfügung. Mit einer PDF-Datei schlagen wir die Brücke zu Print, weil wir beliebig skalierbare Daten herstellen. Damit können wir beispielsweise Buchstabenbilder in Plakatgröße drucken.
Pixelbild
void setup() { size (800, 800); noLoop(); } void draw() { background (0); ellipse (400, 400, 200, 200); save ("data/kreis.tif"); }
Vektorbild
import processing.pdf.*; void setup() { size (800, 800); noLoop(); } void draw() { beginRecord(PDF, "data/kreis.pdf"); background (0); ellipse (400, 400, 200, 200); endRecord(); }
Aufgaben
Export / Aufgabe 1
Verwende den Code "Vektorbild". Kopiere einen Code deiner Wahl aus den bisherigen Aufgaben und exportiere diesen als PDF. Öffne die entstandene Datei in Illustrator. Bevor du die Daten verändern kannst, musst du zunächst mit dem Inhaltswerkzeug einen mehrfachen Rahmen um die Grafik herum löschen. Danach kommst du an die einzeilen Vektorformen dran und kannst diese verändern oder weitere Formen in Illustrator hinzufügen.
Export
Wir können Processinggrafiken als Bilddaten oder Vektordaten exportieren. Vektordaten sind beliebig skalierbar. Wenn wir Standbilder erzeugen wollen, sollten wir Vektordaten verwenden. Dazu exportieren wir PDFs. Hierzu umklammern wir das grafische Material mit der Methode beginRecord und endRecord. Was sich nach beginRecord befindet landet in der Datei, alles davor dagegen nicht: Vorsicht bei Attributen, die im setup-Bereich stehen. Diese bleiben beim Export unberücksichtigt. Wenn wir Vektordaten in Illustrator öffnen, entfernen wir einen mehrfachen Inhaltsrahmen mit dem weißen Inhaltswerkzeug, bevor wir separate Formen verschieben können.
zurück zur Übersicht–––
Einfachschleife
Video
Wie wiederholen wir mit einer Schleife Elemente ?
Mit Schleifen wiederholen wir beliebig oft Teile eines Programms. Zusammen mit Variablen, die ihren Wert im Laufe eines Programms verändern, bauen wir Grafik unter Verwendung eines Elements schrittweite auf. Während wir while-Schleifen im Aufbau und Ablauf leichter nachvollziehen können, sind for-Schleifen kompakter und übersichtlicher. Nützlich werden for-Schleifen vor allem wenn wir zwei oder mehr davon miteinander kombinieren. Schleifen sind das elementare Instrument, wenn es darum geht, Prozesse zu automatisieren.
Schleifenarten
while-Schleife int x = 40; while (x <= 60) { point (x, 50); x = x + 10; } for-Schleife for (int x = 40; x <= 60; x = x + 10) { point (x, 50); }
Konzentrische Wiederholung

size(800, 800); noFill(); float radius = 50; while (radius < 600) { ellipse(400, 400, radius, radius); radius = radius + 50; }
Horizontale Wiederholung

size(800, 800);
fill(0);
float radius = 8;
for (int x = 40; x <= 760; x = x + 40) {
ellipse (x, 400, radius, radius);
}
Vertikale Wiederholung

size(800, 800);
fill(0);
float radius = 8;
for (int y = 40; y <= 760; y = y + 40) {
ellipse (400, y, radius, radius);
}
Übung Schleife


Gruppenarbeit: Orientiert euch am Beispielcode. Schreibt gemeinsam zunächst ein Programm, das vier Kreise horizontal zeichnet. Verwendet dazu eine Schleife und Variable. Schreibt danach das Programm um, damit es vier Kreise vertikal zeichnet.
for (int a = 10; a < 50; a = a + 10) {
noFill();
// ellipse (50, 50, 15, a);
// ellipse (50, 50, a, 15);
// ellipse (50, a, 15, 15);
// ellipse (a, 50, 15, 15);
// ellipse (50, 50, a, a);
}
Übung Schleife und Hilfsvariable

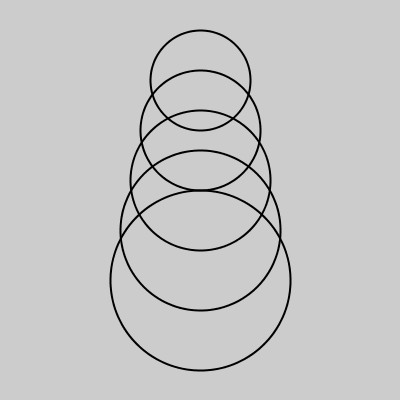
Gruppenarbeit: Orientiert euch am Beispielcode. Schreibt gemeinsam zunächst ein Programm, das vier Kreise horizontal zeichnet, die größer werden. Verwendet dazu eine Schleife, Variable und eine Hilfsvariable. Schreibt danach das Programm um, damit es vier Kreise vertikal zeichnet, die größer werden.
int b = 15;
for (int a = 10; a < 50; a = a + 10) {
noFill();
...
b = b + 5;
}
Übung Schleife, Hilfsvariable und if-Abfrage

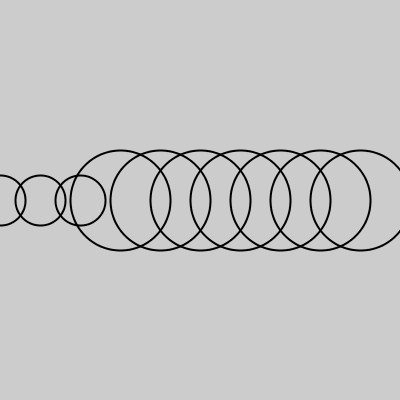


Gruppenarbeit: Orientiert euch am Beispielcode. Verändert zunächst die Bedingung in der if-Abfrage.
int b;
for (int a = 0; a <= 100; a = a + 10) {
if (a < 50) b = 15; else b = 30;
noFill();
ellipse(a, 50, b, b);
}
Aufgaben
Einfachschleife / Aufgabe 1a bis 1c



Kopiere den Code "Horizontale Wiederholung" und modifiziere ihn. Verdopple in der ersten Aufgabe den Abstand zwischen den Punkten. Halbiere in der zweiten Aufgabe den Abstand zwischen den Punkten. Verkürze in den dritten Aufgabe den Start- und Endpunkt der horizontalen Wiederholung.
Einfachschleife / Aufgabe 2a bis 2c



Verwende für Aufgabe 2a die Lösung aus Aufgabe 1c und modifiziere diese. Verschiebe in Aufgabe 2b deine vertikale Wiederholung nach links. Verschiebe in Aufgabe 2c deine vertikale Wiederholung nach rechts.
Einfachschleife / Aufgabe 3a und 3b

Verwende in 3a eine for-Schleife und zeichne damit zwei Punktreihen. Einmal in Rot und einmal in Blau. Verwende in Aufgabe 3b die Lösung aus Aufgabe 3a und erweitere diese. Füge in die vorhandene for-Schleife schwarze Linien hinzu. Deine Linien zeichnest du entweder von rot nach blau oder von blau nach rot.
Einfachschleife / Aufgabe 4a und 4b
+
-


In Aufgabe 4a brauchst du neben der einfachen Schleife für die Position der Linie eine zusätzliche Variable für die Höhe der Linie. Dreh den Höhenverlauf in Aufgabe 4b um.
In Aufgabe 4a brauchst du neben der einfachen Schleife für die Position der Linie eine zusätzliche Variable für die Höhe der Linie. Erstelle dazu einen "Handshake" für die Variable hoehe mit dem Datentyp float. Zeichne die Linien von unten nach oben und von links nach rechts. Verwende eine einfache Schleife mit der Variable x, um die x-Koordinate des Anfangspunktes der Linie zu bestimmen. Die y-Koordinate bleibt konstant. Bei einer Zeichenfläche von 800 mal 800 Pixeln würde die y-Koordinate 800 betragen. Den Endpunkt der Linie bestimmst du relativ zum Anfangspunkt mit Hilfe einer Parametersubtraktion. Du subtrahierst dazu die Variable hoehe. Nun musst du noch innerhalb der Schleife mit einer Variablensubtraktion den Wert der Variable Höhe verändern.
Schleife
Mit bereits drei Zeilen Code können wir eine unzählbare Menge an Elementen mit einer Schleife erzeugen. Es ist offensichtlich, dass sich hier die eigentliche Stärke von Processing zeigt. Um ein Element zu wiederholen, definieren wir einen Parameter des Elements als Variable. Die Wiederholung bezieht sich auf den Wert dieser Variable. Der Wert hat einen Anfangspunkt, einen Endpunkt und eine Schrittweite. Die Schrittweite entscheidet, wie viele Elemente erzeugt werden, bis der Endpunkt erreicht wird. Die Schrittweite wird meistens mit einer Variablenaddition angegeben. Eine Schleife hat eine Abbruchbedingung, die ihr Ende bewirkt. Dabei wird der aktuelle Wert der Variable mit dem Endwert in einer Bedingung verglichen. Meistens vergleicht die Bedingung, ob der aktuelle Wert der Variable den Endwert erreicht. Solange das Ergebnis der Bedingung wahr ist, wiederholt die Schleife ihren Inhalt.
Struktur
Innerhalb eines linearen Aufbau eines Programm bewirkt eine Schleife, dass bestimmte Teile unseres Codes in einer geordneten Zahl wiederholt werden. Wiederholt wird, was sich im Schleifenkörper befindet. Geschweifte Klammern markieren dabei eine oder mehrere Zeilen. Der Schleifenkopf bestimmt die Anzahl der Wiederholungen. Den Schleifenkopf erkennen wir an der Methode for.
zurück zur Übersicht–––
Doppelschleife
Video
Wie erstellen wir ein Muster mit einer Doppelschleife ?
Um grafische Muster als Flächen aufzubauen, verwenden wir zwei Schleifen, die wir miteinander verbinden. Die ineinander geschachtelten Schleifen verhalten sich wie zwei Zahnräder – ein großes Zahnrad mit einem kleinen zusammen. Das kleine Zahnrad dreht sich viel öfter als das große. Die mechanische Logik dieses Systems verwenden wir, um ein grafisches Muster in der Fläche entweder zeilenweise oder spaltenweise aufzubauen. Um Muster zu modulieren verwenden wir zusätzlich zum Zahnräderwerk Hilfsvariablen, die mit dem Zahnräderwerk mitlaufen.
Horizontale Wiederholung

size(800, 800);
fill(0);
float radius = 8;
for (int x = 40; x < 800; x = x + 40) {
ellipse (x, 400, radius, radius);
}
Horizontale Laufvariable

size(800, 800);
fill(0);
float radius = 2;
for (int x = 40; x < 800; x = x + 40) {
ellipse (x, 400, radius, radius);
radius = radius + 2;
}
Muster

size(800, 800);
fill(0);
float radius = 8;
for (int x = 40; x < 800; x = x + 40) {
for (int y = 40; y < 800; y = y + 40) {
ellipse (x, y, radius, radius);
}
}
Flächenlaufvariable

size(800, 800);
fill(0);
float radius = 2;
for (int x = 40; x < 800; x = x + 40) {
for (int y = 40; y < 800; y = y + 40) {
ellipse (x, y, radius, radius);
radius = radius + 0.1;
}
}
Übung Doppelschleife



Gruppenarbeit: Ergänzt die fehlende Zeile. Verwendet dazu die beiden Variablen a und b sowie einen absoluten Wert für den Durchmesser der Kreise. Wie verhält sich der Durchmesser der Kreise im Vergleich zum Schrittweite der for-Schleifen ?
for (int a = 20; a <= 60; a = a + 20) {
for (int b = 20; b <= 60; b = b + 20) {
noFill();
...
}
}
Übung Doppelschleife und if-Abfrage



Gruppenarbeit: Ergänzt die fehlenden Stellen und die fehlende Zeile. Verwendet dazu die beiden Variablen a und sowie eine Variable d für den Durchmesser der Kreise.
int d = 8;
for (int a = 20; a <= 80; a = a + 10) {
for (int b = 20; b <= 80; b = b + 10) {
noFill();
if (...) ...; else ...;
...
}
}
Übung Doppelschleife und Hilfsvariable mit spaltenweisem Aufbau

Gruppenarbeit: Ergänzt die fehlenden Zeilen. Verwendet die Hilfsvariable d und eine Variablenaddition für d, um die Kreise stetig zu vergrößern. Ist es besser die Variablenaddition in die äußere oder in die innere Schleife zu setzen ?
int d = 8;
for (int a = 20; a <= 80; a = a + 10) {
for (int b = 20; b <= 80; b = b + 10) {
noFill();
...
...
}
...
}
Übung Doppelschleife und Hilfsvariable mit zeilenweisem Aufbau

Gruppenarbeit: Verwendet statt einem spaltenweisem Aufbau einen zeilenweisen Aufbau.
int d = 8;
for (int a = 20; a <= 80; a = a + 10) {
for (int b = 20; b <= 80; b = b + 10) {
noFill();
...
...
}
...
}
Aufgaben
Doppelschleife / Aufgabe 1a bis 1c



Kopiere den Code "Muster". Verdopple in Aufgabe 1a die Punktabstände sowohl in horizontaler als auch in vertikaler Richtung. Halbiere in Aufgabe 1b die Punktabstände sowohl in horizontaler als auch in vertikaler Richtung. Verändere in Aufgabe 1c Start- und Endwerte des Musters.
Doppelschleife / Aufgabe 2a und 2c



Kopiere den Code "Muster". Verdopple in Aufgabe 2a die Punktabstände in vertikaler Richtung. Verdopple in Aufgabe 2b die Punktabstände in horizontaler Richtung. Verwende in 2c die doppelte Schleife um den Anfangspunkt der Linie zu bestimmen. Den Endpunkt der Linie bestimmst du relativ zum Anfangspunkt mit einer Parameteraddition und Parametersubtraktion.
Doppelschleife / Aufgabe 3
+
-

Kopiere den Code "Flächenlaufvariable" und verändere den Verlauf in die entgegengesetzte Richtung. Finde dazu mit der Methode println heraus, welchen Wert die Variable radius am Ende des Programms hat.
Kopiere den Code "Flächenlaufvariable" und verändere den Verlauf in die entgegengesetzte Richtung. Um das zu erreichen könntest du zunächst herausfinden welchen Wert die Variable radius am Ende des Programms hat - füge dazu als letzte Zeile die Methode println mit der Variable radius als Parameter hinzu. Verwende den so ermittelten Wert als Startwert für die Variable radius. Wandle die Variablenaddition in eine Variablensubtraktion um.
Doppelschleife / Aufgabe 4
+
-

Kopiere den Code "Muster". Zeichne Kreise statt Punkte. Füge drei Laufvariablen rot, gruen und blau hinzu. Verwende die neuen Laufvariablen um deine Kreise mit einer Verlaufsfarbe zu füllen. Achte darauf, dass der Endwert deiner Laufvariablen 255 nicht übersteigt oder 0 nicht unterschreitet.
Kopiere den Code "Muster". Zeichne Kreise statt Punkte. Erstelle zunächst "Handshakes" für drei Laufvariablen rot, gruen und blau. Verwende dabei als Datentyp "float". Weise diesen Laufvariablen zunächst den Startwert 0 zu. Erhöhe innerhalb der Schleife mit einer Variablenaddition für jede der drei Laufvariablen ihren Wert. Du kannst hier durchaus sehr geringe Werte mit Nachkommastellen wählen wie zum Beispiel 0.2 oder 0.05. Das hängt ganz davon ab wie schnell sich ein Farbanteil verändern soll. Wichtig ist, das du für jede Laufvariable einen anderen Wert wählst, damit sich Farbe überhaupt bilden kann. Bei gleichen Wert für alle drei Laufvariablen würdest du lediglich Graustufen erzeugen. Bevor du die Methode ellipse anwendest, legst du mit der Methode fill und den den drei Laufvariablen die Farbe deines Kreises fest. Du kannst den Farbverlauf eines Farbanteils umgekehrt anlegen. Als Startwert wählst du dafür 255 und erniedrigst innerhalb der Schleife die Laufvariable mit einer Variablensubtraktion. Die besten Ergebnisse bekommst du mit einer Mischung aus Laufvariablen mit aufsteigender und absteigender Wertveränderung. Ein Farbanteil sollte weder den Wert 255 übersteigen noch den Wert 0 unterschreiten. Befindet sich ein Farbanteil außerhalb des Bereichs erzeugt die Methode fill zwar keinen Fehler, jedoch produziert sie auch keine Farbe mehr. Stattdessen sehen wir, dass die Farbe weiss oder schwarz verbleibt. Um den Wert zu überprüfen, den die Laufvariablen annehmen, fügst du die Methode println hinzu und wählst als Parameter den Namen der Laufvariable.
Laufvariable
In einem Schleifenkopf kann immer nur eine Variable definiert werden, deren Wert sich im Verlauf der Schleife verändert. Wenn wir innerhalb der gleichen Schleife eine weitere Variable einsetzen wollen, brauchen wir eine Hilfskonstruktion in Form einer Laufvariablen. Dazu erstellen wir einen Handshake für diese Variable vor der Schleife und weisen ihr einen Anfangswert zu. Im Schleifenkörper erstellen wir eine Variablenaddition. Dadurch koppeln wir unsere Laufvariable an die bestehende Schleifenkonstruktion und stellen sicher, dass sich unsere zusätzliche Variable ebenfalls in ihrem Wert verändert.
Doppelschleife
Fügen wir eine zweite Schleife in den Schleifenkörper der ersten hinein, verhält sich die Gesamtkonstruktion wie zwei zusammenhängende Zahnräder. Die äußere Schleife wird zum großen Zahnrad, die innere Schleife zum kleinen Zahnrad. Typischerweise verwenden wir solche Doppelschleifen um eine Fläche in horizontaler und vertikaler Richtung mit einem Element zu füllen. Kombinieren wir die Möglichkeiten von Schleifen zum Aufbau von Mustern mit der Möglichkeit von Laufvariablen, können wir monotone Fläche modulieren. Erste Modulationen können wir bereits mit den vier Grundrechenarten wie Variablenaddition, Variablensubtraktion, Variablenmultiplikation und Variablendivision herbeiführen. Wir könnten beispielsweise die Kreisgröße während eines Flächenaufbaus verändern. In den weiteren Kapiteln werden noch weitere Modulationsmöglichkeiten kennenlernen.
zurück zur Übersicht–––
Rauschen
Video
Wie generieren wir realistische Zufallszahlen ?
Um ein Muster lebendig zu gestalten, brauchen wir einen digitalen Zufallsgenerator. Noise ist an natürliche Prozesse wie Wolken oder Rauch angelehnt und liefert uns glaubwürdige Zufallszahlen, die auch in einer zweidimensionalen Fläche unser Muster glaubwürdig modulieren können. Einen einmal erzeugten Zufallsgenerator können wir auf einen bestimmten Parameter unser generativen Grafik anwenden und diesen über die Fläche modulieren. Je mehr Zufallsgeneratoren wir erzeugen, desto mehr Parameter können wir modulieren und desto lebendiger wird unsere generative Grafik.
Noise

float off; float schrittweite = 0.005; size(800, 800); off = 0; for (int x = 0; x < 800; x = x + 1) { off = off + schrittweite; float zufallszahl = map(noise(off),0,1,0,800); point (x, zufallszahl); }
Noisemuster

float xoff, yoff; float schrittweite = 0.2; size(800, 800); xoff = 0; for (int x = 40; x < 800; x = x + 40) { xoff = xoff + schrittweite; yoff = 0; for (int y = 40; y < 800; y = y + 40) { yoff = yoff + schrittweite; float radius = map(noise(xoff, yoff),0,1,10,40); ellipse (x, y, radius, radius); } }
Zwei Zufallszahlen

float offset1 = 0; float offset2 = 0; size(800, 800); for (int x = 0; x < 800; x = x + 1) { float zufallszahl1 = map(noise(offset1),0,1,0,400); float zufallszahl2 = map(noise(offset2),0,1,10,410); point (x, zufallszahl1); point (x, zufallszahl2); offset1 = offset1 + 0.005; offset2 = offset2 + 0.004; }
Methode noise
Das Ergebnis der Methode noise liegt zwischen 0 und 1 und wird in der Variable noiserauschen gespeichert. Damit die Methode noise funktioniert, braucht sie einen Parameter, der hier offset heißt. Das Ergebnis der Methode noise verändert sich nur wenn wir ihren Parameter offset durch eine Variablenaddition verändern. Für gute Ergebnisse stellen wir eine Wert zwischen 0.03 und 0.005 für die Variablenaddition ein. Um das Ergebnis der Methode noise verwenden zu können, müssen wir es meistens vergrößern. Um das Ergebnis zu vergrößern können wir uns der Methode map bedienen. Sie skaliert für uns den Wertebereich der Noisefunktion – der zunächst immer zwischen 0 und 1 liegt – auf den von uns gewünschten Zielbereich, hier im Beispiel zwischen 10 und 40. Das Mapping des Wertebereichs können wir uns wie einen Pullover vorstellen, der entweder im Trocker schrumpft oder durch Ziehen vergrößert wird. Alle Werte dazwischen passen sich entsprechend an. In unserem Beispiel wird aus einer ursprünglichen 0.5 die genau zwischen 0 und 1 liegt, eine 25 die genau zwischen 10 und 40 liegt. float offset = 0; for (int anz = 0; anz < 10; anz = anz + 1) { float noiserauschen = map(noise(offset),0,1,10,40); println("noise: " + noiserauschen); offset = offset + 0.03; }
Methode map
Noise erzeugt immer sehr kleine Zufallszahlen zwischen 0 und 1. Der Unterschied zwischen gar keinem und einem Pixel ist visuell so gut wie unsichtbar. Wir verwenden die Methode map, um die Ergebnisse von noise zu vergrößeren. float eingabe = noise(0.1); float minEingabe = 0; float maxEingabe = 1; float minAusgabe = 0; float maxAusgabe = 255; float ausgabe = map(eingabe, minEingabe, maxEingabe, minAusgabe, maxAusgabe); println("eingabe", eingabe); println("ausgabe", ausgabe);
Übung Mapping
Die Methode map ist eine Funktion. Wir übergeben ihr den Wert eingabe und erhalten den Wert ausgabe. Der Funktion map teilen wir mit, welchen Wert eingabe minimal und maximal erreichen kann. In unserem Beispiel minimal 0 und maximal 1. Der Funktion map teilen wir ebenfalls mit, welchen Wert ausgabe minimal und maximal erreichen kann. In unsrem Beispiel minimal 10 und maximal 20.
float eingabe = 0.5;
float ausgabe = map(eingabe, 0, 1, 10, 20);
println("ausgabe", ausgabe);
Besprecht euch in der Gruppe. 01 Welchen Wert erzeugt das Programm aktuell für ausgabe ? 02 Welchen Wert brauchen wir für eingabe um 10 für ausgabe zu erhalten ? 03 Welchen Wert brauchen wir für eingabe um 12.5 für ausgabe zu erhalten ? 04 Wir wollen für ausgabe Werte zwischen -25 und 25 erhalten. Wo tragen wir das ein ? 05 Wir werden für eingabe Werte zwischen -1 und 1 erhalten. Wo tragen wir das ein ?
Übung Noise
Starte das Programm einige Male und beobachte das Ergebnis.
float a = noise(0.1); float b = noise(0.1); println("a", a); println("b", b);
01 Warum erzeugt das Programm immer die gleiche Zufallszahl für a und b ? 02 Wie können wir zwei Zufallszahlen für a und b innerhalb eines Programmaufrufs erzeugen ?
Aufgaben
Rauschen / Warmup
Starte das Codebeispiel Noise mehrfach und beobachte das Ergebnis. Warum verändert sich bei jedem Aufruf das Ergebnis ? Verändere nun die Zahl die offset hinzuaddiert wird – stellt hier Zahlen zwischen 0.03 und 0.005 ein. Wie wirkt sich die Veränderung auf den Kurvenverlauf aus ? Um die Charakteristik des Rauschens beim Codebeispiel Noisemuster zu verändern, veränderst du den Wert von schrittweite. Stell hier verschiedene Werte ein und probier auch mal Werte zwischen 0.03 und 0.005 einzustellen anstatt 0.2. Warum ist 0.2 als Wert hier passend ?
Rauschen / Aufgabe 1a bis 1c
+
-



Kopiere das Codebeispiel Noise. Wende in 1a die Zufallszahl auf den Radius eines Kreises an. Wende in 1b die Zufallszahl auf das Ende einer Linie an. Füge in 1c eine zweite Zufallszahl für den Anfang einer Linie hinzu.
Kopiere das Codebeispiel Noise. Wende in 1a die Zufallszahl auf den Radius eines Kreises an. Wende in 1b die Zufallszahl auf das Ende einer Linie an. Füge in 1c eine zweite Zufallszahl für den Anfang einer Linie hinzu. Der Wert, den du der Variable offset hinzuaddierst, entscheidet über das Aussehen der Grafik oder darüber ob sich überhaupt etwas in der Grafik verändert. Wenn du keine Veränderung in deiner Grafik erkennen kannst, solltest du diesen Wert verändern. Normalerweise gibst du hier Werte zwischen 0.03 und 0.005 an, manchmal sind auch größere Werte wie 0.2 oder 2 sinnvoll. Es kommt auf die Anzahl der Elemente an, die du abbildest, welcher Wert sinnvoll ist. Wählst du den Wert zu klein, wirst du kaum Veränderung erkennen. Wählst du den Wert zu groß, werden die Sprünge zu groß. Die Methode noise liefert dir immer Zufallswerte zwischen 0 und 1, zum Beispiel 0.12987 oder 0.72390. Mit der Methode map skalierst du die Zufallswerte auf einen gewünschten Bereich – einem Minimum und Maximum. Wenn du zum Beispiel zufällige Werte zwischen 0 und 800 für den Radius deines Kreises brauchst, fügst du 0 und 800 als vierten und fünften Parameter in die Methode map ein. Die tatsächlich erzeugten Zufallswerte werden zwischen 0 und 800 liegen, werden jedoch nicht immer den gesamten Bereich aussfüllen. Sie könnten zum Beispiel zwischen 400 und 650 liegen. Und sie können sich mit jedem neuen Start des Programms ändern. Mit dem vierten und fünften Paramter von map legst du nur mögliche Grenzen fest, sagt noch nichts über die tatsächlichen Werte aus. In Aufgabe 1b zeichnest du die Linien von unten nach oben und von links nach rechts. Die einfache Schleife verwendest du für die x-Position des Anfangspunktes der Linie. Die y-Position bleibt konstant auf 800 bei einer Zeichenfläche von 800 mal 800 Pixeln. Den Endpunkt der Linie bestimmst du relativ zum Anfangspunkt mit einer Parametersubtraktion. Die Zufallszahl subtrahierst du dabei von der y-Position des Anfangspunktes der Linie. In Aufgabe 1c kopierst du den Code "Zwei Zufallszahlen" und passt ihn entsprechend an.
Rauschen / Aufgabe 2a bis 2c
+
-



Kopiere das Codebeispiel Noisemuster. Wende in Aufgabe 2a das Rauschen auf die Strichstärke statt auf den Radius an. Wende in Aufgabe 2b das Rauschen auf das Linienende an. Für den Linienbeginn nimmst du die Variablen x und y. Mit einer Parameteraddition und Parametersubtraktion bestimmst du das Linienende relativ zum Linienbeginn. In Aufgabe 2c brauchst du eine Zufallszahl für den Grünanteil der Farbe und eine zweite Zufallszahl für den Blauanteil der Farbe. Den Rotanteil kannst du konstant auf den Wert 0 setzen.
Kopiere das Codebeispiel Noisemuster. Wende in Aufgabe 2a das Rauschen auf die Strichstärke statt auf den Radius an. Wende in Aufgabe 2b das Rauschen auf das Linienende an. Für den Linienbeginn nimmst du die Variablen x und y. Mit einer Parameteraddition und Parametersubtraktion bestimmst du das Linienende relativ zum Linienbeginn. In Aufgabe 2c brauchst du eine Zufallszahl für den Grünanteil der Farbe und eine zweite Zufallszahl für den Blauanteil der Farbe. Den Rotanteil kannst du konstant auf den Wert 0 setzen. Im Codebeispiel Noisemuster wird die Zufallszahl in der Variable radius gespeichert. Wenn du deine Zufallszahl für andere Zwecke einsetzen möchtest, solltest du deine Zufallszahl entsprechend umbenennen. In Aufgabe 2a ersetzt du am Besten den Variablennamen radius durch strichstaerke. Jetzt passt du den Wertebereich der Methode noise für deine Zwecke an. Eine sinnvolle Strichstärke befindet sich zwischen 0 und 10 Punkten. Das bedeutet, dass du die Methode noise mit 10 multiplizieren solltest. Um die Strichstärke auf einen Kreis anzuwenden musst vor der Methode ellipse die Methode strokeWeight mit strichstaerke als Parameter anwenden. In Aufgabe 2b verwendest du die doppelte Schleife um den Anfangspunkt deiner Linie zu bestimmen. Den Endpunkt der Linie bestimmst du relativ zum Anfangspunkt. Dazu erstellst du eine einzige Zufallszahl. Diese addierst einmal zu x mit einer Parameteraddition. Diese subtrahierst du zweitens von y mit einer Parametersubtraktion. Deine Zufallszahl orientiert sich an der Rasterweite deiner Doppelschleife. Wenn du beispielweise 40 Pixel Abstand zwischen deinen Elementen festlegt, schreibst du in map 0 und 40 als vierten und fünften Parameter. Bei 15 Pixel Abstand als Beispiel, würdest du in map 0 und 15 eintragen. So werden sich deine diagonalen Linien höchstens berühren. In Aufgabe 2c überträgst du die Struktur aus dem Code "Zwei Zufallszahlen" auf den Code "Noisemuster". Die Variable radius ersetzt du durch die Variable gruen. Passend dazu benennst du xoff, yoff und schrittweite in xoff1, yoff2 und schrittweite1 um. Für die Variable blau erstellt du weitere Variablen xoff2, yoff2 und schrittweite2 an. Für den blauen und grünen Farbkanal brauchst du Werte zwischen 0 und 255. In map verwendest du dafür 0 als vierten und 255als fünften Parameter. Farbig wird deine Grafik erst wenn du unterschiedliche Schrittweiten für deine Farbkanäle einstellst.
Funktion
Die Methode noise gleicht einer mathematischen Funktion. noise erwartet als Parameter einen Wert und gibt als Ergebnis eine Zufallszahl zwischen 0 und 1 zurück. Wie bei anderen stetigen Funktionen auch, wird jedem Eingabewerte exakt ein Ausgabewert zugeordnet. Für jeden Wert, den wir als Parameter noise übergeben, erhalten wir exakt eine Zufallszahl zurück. Bei gleichbleibendem Wert, bleibt die Zufallszahl auch gleich. Um unterschiedliche Zufallszahlen zu erhalten, müssen wir den Wert verändern, den wir an die Methode noise als Parameter übergeben. Typischerweise legen wir für den Eingabewert eine Laufvariable an, die meistens offset heißt. Die Laufvariable verändern wir innerhalb einer Schleife mit einer Variablenaddition. Der Wert der Laufvariable wird erst durch die Methode noise in eine Zufallszahl umgewandelt. Im Ergebnis wandeln wir eine gleichmäßige Zahlenreihe in eine zufällige um. Ein zufälliges Ergebnis zwischen 0 und 1 ist jedoch so klein, dass es fast immer durch eine Mapping angepasst werden muss. Dieser Vorgang ist mit einem Pullover vergleichbar den wird entweder dehnen oder im Trocker bewußt schrumpfen.
Zweidimensionaler Noise
In einer Doppelschleife brauchen wir einen zweidimensionalen Noise mit zwei Parametern statt einem: den ersten für die x-Achse, diesen nennen wir beispielsweise xoff, den zweiten für die y-Achse, diesen nennen wir beispielsweise yoff. Beide Parameter koppeln wir an den Aufbau des eigentlichen Musters. Die äußere Schleife des Musters bestimmt die x-Koordinate unseres Elements, die innere Schleife die y-Koordinate. xoff koppeln wir an die x-Koordinate, yoff an die y-Koordinate. Für xoff machen wir einen Handshake vor der äußeren Schleife. Wir weisen ihm zur gleichen Zeit einen Anfangswert zu. Den Wert von xoff erhöhen wir innerhalb der äußeren Schleife mit einer Variablenaddition. Für yoff machen wir einen Handshake vor der inneren Schleife. Wir weisen ihm zur gleichen Zeit ebenfalls einen Anfangswert zu. Den Wert von yoff erhöhen wir innerhalb der inneren Schleife mit einer Variablenaddition. Die Methode noise rufen wir in der inneren Schleife auf. Obwohl wir noise zwei Parameter übergeben, erhalten wir dennoch nur eine einzige Zufallszahl zurück. Jedoch ist diese Zufallszahl sowohl harmonisch zu ihren vertikalen als auch horizontalen Nachbarn in einem zweidimensionalen grafischen Muster. Im Gegensatz dazu nimmt random keine Rücksicht auf seine Nachbarn und baut auch keinen Bezug zu ihnen auf.
Mapping
Die Methode noise erzeugt Zufallszahlen zwischen 0 und 1 mit etlichen Nachkommastellen. Diese Werte sind sehr klein. Eine Modulation zwischen einem und gar keinem Pixel ist visuell fast unsichtbar. Um die ursprünglichen Zufallszahlen von Noise für visuelle Zwecke anzuwenden, skalieren wir die Ergebnisse mit der Methode map. Map braucht fünf Parameter. Für den ersten Parameter setzen wir die Ergebnisse der Methode noise ein. Den zweiten und dritten Parameter von map passen wir an die möglichen minimalen und maximalen Ergebnisse von noise an. Bei noise liegen die Ergebnisse minimal bei 0 und maximal bei 1. Diese Angaben finden wir in der Referenz zur Methode noise. Im vierten und fünften Parameter von map notieren wir den minimalen und maximalen Wert, den unser Mapping erreichen soll. Für einen Farbanteil würden wir beispielsweise im vierten und fünften Parameter 0 und 255 notieren. Für eine Strichstärke dagegen einen Wert zwischen 0 und 10. Für einen Radius einen Wert zwischen 20 und 50. Für die x-Position eines Elements –25 und 25. Mit map lassen sich die Ergebnisse von noise sehr bequem anpassen. Einfach den vierten und fünften Parameter von map verändern und den zufällig erzeugten Wertebereich an die jeweilige Situation anpassen. Der zweite und dritte Parameter von map bleibt immer gleich. Solange wir noise als ersten Parameter verwenden, bleiben die primären Ergebnisse von noise immer zwischen 0 und 1.
float output = map(input, minInput, maxInput, minOutput, maxOutput);
Weiterführende Themen
Wenn du die Noisefunktion verwenden kannst, bist du auch in der Lage eine Sinusfunktion sin() einzusetzen. Die Sinusfunktion erwartet als Eingabewert einen ins Bogenmaß umgerechneten Winkel – zum Beispiel radians(45). Als Ausgabe erhälst du einen Wert zwischen -1 und 1.
Die Methode map() vereinfacht den Einsatz der Noise- und Sinusfunktion. Mit map() kannst das Ergebnis einer Funktion auf einen anderen Wertebereich automatisch umrechnen lassen. map(noise(offset), 0, 1, -10, 32) rechnet das Ergebnis der Noisefunktion mit dem Eingabewert offset - das zwischen 0 und 1 liegt - automatisch auf einen Wertebereich zwischen -10 und 32 um.
–––
Buchstabe
Video
Wie schneiden wir aus einem Muster einen Buchstaben aus ?
Ein Muster erstellen wir mit einer Doppelschleife. Unter dieses Muster legen wir einen einzelnen Buchstaben. Mit einem digitalen Durchpaustrick schneiden wir aus dem Muster den hinterlegten Buchstaben heraus. Der flächige Buchstabe besteht danach aus dem zuerst erzeugten Muster – so gestalten wir einen Buchstaben als Fläche. Um die Kontur eines Buchstabens mit Elementen zu zeichnen, brauchen wir in Processing die externe Library geomerative. Sie liefert uns die Konturkoordinaten eines Buchstabens als Container.
Buchstabenoutline

import geomerative.*;
RShape gruppe;
RPoint[] p;
void setup() {
size (800,800);
noLoop();
RG.init(this);
gruppe = RG.getText("R",
"DINOT-Bold.ttf", 800, CENTER);
RG.setPolygonizer (RG.UNIFORMLENGTH);
p = gruppe.getPoints();
}
void draw() {
translate (width/2-50, height/2+275);
for (int n = 0; n < p.length; n = n + 3) {
ellipse (p[n].x, p[n].y, 6, 6);
}
}
Buchstabenfläche

PGraphics bild; PFont schrift; void setup() { size(800, 800); noLoop(); bild = createGraphics(width, height); schrift = createFont("DINOT-Bold.otf",800); bild.beginDraw(); bild.background(255); bild.fill(0); bild.textFont(schrift); bild.textSize(800); bild.textAlign(CENTER, CENTER); bild.text("R", bild.width/2, bild.height/2); bild.endDraw(); } void draw() { for (int x = 0; x < 800; x = x + 15) { for (int y = 0; y < 800; y = y + 15) { if (bild.get (x, y) == color(0)) { stroke(0); line (x, y, x + 8, y - 8); } } } }
Outline mit 1D-Noise

import geomerative.*;
RShape gruppe;
RPoint[] p;
float offset = 0;
float schrittweite = 0.05;
void setup() {
size (800,800);
noLoop();
RG.init(this);
gruppe = RG.getText("R",
"DINOT-Bold.ttf", 800, CENTER);
RG.setPolygonizer (RG.UNIFORMLENGTH);
p = gruppe.getPoints();
}
void draw() {
translate (width/2-50, height/2+275);
for (int n = 0; n < p.length; n = n + 3) {
float lg = map(noise(offset),0,1,0,200);
line (p[n].x, p[n].y, p[n].x + lg, p[n].y - lg);
offset = offset + schrittweite;
}
}
Fläche mit 2D-Noise

PGraphics bild; PFont schrift; float xoff, yoff; float schrittweite = 0.2; void setup() { size(800, 800); noLoop(); bild = createGraphics(width, height); schrift = createFont("DINOT-Bold.otf",800); bild.beginDraw(); bild.background(255); bild.fill(0); bild.textFont(schrift); bild.textSize(800); bild.textAlign(CENTER, CENTER); bild.text("R", bild.width/2, bild.height/2); bild.endDraw(); } void draw() { xoff = 0; for (int x = 0; x < 800; x = x + 15) { xoff = xoff + schrittweite; yoff = 0; for (int y = 0; y < 800; y = y + 15) { yoff = yoff + schrittweite; if (bild.get (x, y) == color(0)) { float radius = map(noise(xoff, yoff), 0, 1, -5, 20); ellipse (x, y, radius, radius); } } } }
Übung Zweite Zeichenfläche
Das Programm erzeugt eine zusätzliche Zeichenfläche mit dem Namen bild. Mit der Methode image machen wir die zusätzliche Zeichenfläche sichtbar.
PGraphics bild; void setup() { size(800, 800); bild = createGraphics(400, 400); bild.beginDraw(); bild.background(255); bild.fill(0); bild.ellipse(200,200,300,300); bild.endDraw(); } void draw() { background(0,0,255); image(bild,0,0); fill(200); noStroke(); ellipse(400,400,200,200); }
01 Erstelle ein leuchtendes Grün für die Hintergrundfarbe der Zeichenfläche bild. 02 Erstelle ein rotes Rechteck in der Zeichenfläche bild. 03 Lösche die Methode image im draw-Bereich.
Übung Schrift
Um Text mit einer eigener Schrift in Processing zu setzen, legst du ein neues Objekt des Typs PFont an. Unser Objekt heißt schrift. Mit CreateFont laden wir im Beispiel die Schrift DINOT-Bold.otf ein.
PFont schrift; void setup() { size(800,800); schrift = createFont("DINOT-Bold.otf",800); textFont(schrift); textSize(800); textAlign(CENTER, CENTER); fill(0); background(255); text("R", 400, 400); }
01 Suche eine Schrift auf deinem Rechner und lade diese in Processing ein.
Übung Vektor
Ein Vektor fasst die x- und y-Koordinate eines Punktes zu einem Objekt zusammen. Die Schreibweise sieht zwar etwas anders aus – den x-Wert oder y-Wert kannst du genauso verändern, als ob es eine Variable wäre.
size(800, 800); PVector p; p = new PVector(400, 400); noFill(); ellipse(p.x, p.y, 300, 300); p.x = p.x + 200; ellipse(p.x, p.y, 300, 300); p.x = 200; ellipse(p.x, p.y, 300, 300);
01 Erstelle einen zweiten Vektor mit dem Namen a. Verwende die Koordinaten von a, um ein Rechteckt zu positionieren.
Übung Array
Ein Array fasst mehrere Variablen zu einem Feld zusammen. Wieviele Elemente ein Array umfasst, bestimmst du selbst – in unserem Beispiel sind es drei Elemente. Die einzelnen Elemente eines Array sprichst du über einen Index an – bei 0 beginnend zu zählen.
float[] x; void setup() { size(800, 800); x = new float[3]; x[0] = 200; x[1] = 400; x[2] = 600; noLoop(); } void draw() { noFill(); ellipse(x[0],200,200,200); ellipse(x[1],400,200,200); ellipse(x[2],600,200,200); }
01 Erstelle ein Array mit drei Elementen für die Durchmesser deiner Kreise. 02 Verwende eine Schleife, um die drei Zeilen zum Zeichnen der Ellipsen zusammenzufassen. Im Schleifenkopf verwendest du für den Index des Arrays eine Variable. Du fängst bei 0 an zu zählen – bis du einschließlich 2 erreichst.
Aufgaben
Installation der Library "geomerative"
Verwende den Code "Buchstabenoutline". Speichere den Code. Erstelle in deinem aktuellem Processingcode-Ordner einen neuen Ordner mit dem Namen "data". Dorthin kopierst du einen Truetype-Font deiner Wahl. Den Dateinamen des Fonts trägst in das Script an der entsprechenden Stelle ein. Bevor du das Programm starten kannst, muss du noch eine Library installieren. im Processing 3 findest du in der Menüzeile unter "Sketch > Library importieren > Library hinzufügen" ein Dialogfenster. In diesem Dialogfenster suchst du nach der Library "geomerative", klickst diese an und löst anschließend den Installiervorgang mit dem entsprechendem Button aus. Danach kannst du das Programm starten.
Buchstabe / Aufgabe 1a und 1b


Verwende den Code "Buchstabenfläche" und "Buchstabenoutline". Zeichne in beiden Fällen statt Diagonalen beziehungsweise Punkten große ungefüllte Kreise, die sich überschneiden.
Buchstabe / Aufgabe 2a und 2b


Verwende den Code "Outline mit 1D-Noise". Verringere in 2a und erhöhe in 2b die Anzahl der Linien. Passe die Schrittweite des Noise an die Anzahl der Linien an. Passe die Strichstärke der Linien ebenfalls an.
Buchstabe / Aufgabe 3

Verwende den Code "Fläche mit 2D-Noise". Zeichne Kreise ohne Füllung mit konstantem Radius. Moduliere die Strichstärke der Kreiskontur mit dem zweidimensionalen Noise.
Buchstabe / Aufgabe 4
+
-

Verwende den Code "Fläche mit 2D-Noise". Die erste Zufallsvariable im Programm heißt radius. Sie basiert auf xoff, yoff und schrittweite. Erstelle eine zweite Zufallsvariable Mx. Sie soll auf xoffMx, yoffMx und schrittweiteMx basieren. Verwende die zweite Variable Mx, um die x-Position der Ellipse zu modulieren – das erreichst du mit einer Parameteraddition x + Mx in der Methode ellipse.
Verwende den Code "Fläche mit 2D-Noise". Die erste Zufallsvariable im Programm heißt radius. Sie basiert auf xoff, yoff und schrittweite. Erstelle eine zweite Zufallsvariable Mx. Sie soll auf xoffMx, yoffMx und schrittweiteMx basieren. Definiere vor dem setup-Bereich die Hilfsvariablen xoffMx, yoffMx und schrittweiteMx. Weise schrittweiteMx vor dem setup-Bereich einen eigenen Wert zu – einen anderen Wert als bei schrittweite. Schaue nun im draw-Bereich nach, an welchen Stellen xoff und yoff Werte zugewiesen werden. Kopiere dieses Vorgehen für xoffMx, yoffMx und lege jeweils eine neue Zeile an. Wenn es zum Beispiel heißt xoff = xoff + schrittweite, schreibst du direkt darunter eine neue Zeile xoffMx = xoffMx + schrittweiteMx. Erstelle nun eine neue Zufallsvariable Mx. Lege Sie nach dem Vorbild der ersten Zufallsvariable radius an. Beachte, dass du statt xoff und yoff nun xoffMx und yoffMx als Parameter für noise brauchst. Verwende die zweite Variable Mx, um die x-Position der Ellipse zu modulieren – das erreichst du mit einer Parameteraddition x + Mx in der Methode ellipse.
Truetype- und Opentype-Schriften
Im Programm Buchstabenoutline lassen sich nur Truetype-Fonts verwenden – also Schriften mit der Endung ttf. Im Programm Buchstabenfläche können wir sowohl Truetype-Fonts als auch Opentypefonts einsetzen – also Schriften mit der Endung ttf und otf. Die meisten Schriften lassen sich in Processing einladen. Manchmal kommt es vor, dass bestimmte Schriften sich nicht einladen lassen.
Buchstabenfläche
Ein Buchstabe wird aus einer Fläche ausgeschnitten. Dazu wird eine zusätzliche unsichtbare Zeichenfläche des Datentyps PGraphics angelegt. Diese ist genauso groß wie die eigentliche Zeichenfläche und liegt auch exakt über der sichtbaren Zeichenfläche. In die unsichtbare Zeichenfläche wird ein einzelner Buchstaben hineingeladen. Der unsichtbare Hintergrund wird weiß gefärbt, der unsichtbare Buchstabe schwarz. Dieser Buchstabe ist so groß, dass er zur Fläche wird. Nun zeichnen wir mit einer Doppelschleife in unsere sichtbare Zeichenfläche ein Muster aus Elementen. Während des Aufbaus unseres Musters wird die Farbe in der unsichtbaren Zeichenfläche mit der Methode get überprüft. In der innere Schleife befindet sich ein Filter mit der Methode if angelegt: Wenn die Farbe schwarz ist, wird ein ein Element in die sichtbare Fläche gezeichnet. Wenn die Farbe weiß ist, bleibt die Stelle frei. Im Ergebnis wird der Buchstabe aus dem unsichtbaren Bereich zu einer Ansammlung von einzelnen Elementen im sichtbaren Bereich.
Buchstabenfläche verändern
Wir haben in den zurückliegenden Aufgaben Flächen gestaltet. Diese können wir nun hier einsetzen. Im einfachen Fall fügen wir unseren Code nach dem Filter ein – eine oder mehrere Zeilen. Manchmal müssen wir auch in die umgebende Struktur der Doppelschleife eingreifen. Wollen wir beispielsweise den zweidimensionalen Noise einsetzen, fügen wir sowohl in die innere Schleife als auch in die äußere Schleife Code ein. Verwenden wir Variablen, müssen wir diese vor dem setup-Bereich mit einem Handshake vorstellen. Eventuell brauchen sie einen Anfangswert.
Weiterführende Themen
Ein Array erkennst du an eckigen Klammern. Hier kannst du über Arrays nachlesen: Array Access Reference Array Tutorial Ein Objekt erkennst du an einem Punkt hinter einem Namen. Hier kannst du über Objekte nachlesen: Dot Reference Object Tutorial Einen Vektor erkennst du an einem .x und .y hinter einem Namen. Hier kannst du über Vektoren nachlesen: PVector Reference PVector Tutorial Die geomerative-Library stellt uns einen neuen Datentyp RPoint zur Verfügung. RPoint ist ein Vektor. RPoint[] ist ein Array mit allen Vektoren der Buchstabenoutline.